Discrete Cosine Transform(DCT)

• What is DCT?

DCT is a lossless transform. Its process can be reversed and will yield the original values - no information is lost. It transforms a signal or image from spatial domain to frequency domain.

DCT can be regarded as axis rotation because it is one of a family of distance preserving transforms. For example, when a image is processed by DCT, the total energy of the values remains constant but only the energy distribution has been changed into a few coefficients.

• How to calculate DCT's coefficients?

In image compression, the basic block is generally an 8*8 array, or 64 pixels.
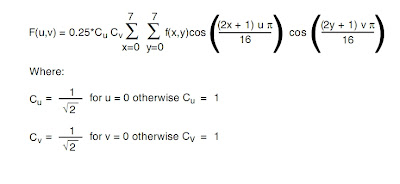The equation is evaluated 64 times, once for each DCT coefficient of the block. Each evaluation uses every one intensity value of pixel of the block, f(x,y).

• Basis Functions

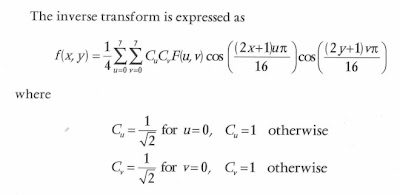
The basis function is the pixel pattern that results when that particular DCT coefficient is set to its maximum value, and all the other coefficients are set to zero.

As a simple example, if F(0,0) is set to 256, and all the others are set to zero, every pixel in the block evaluates to 32. F(0,0) is also called DC coefficient, or a scaled average value of the block.

The basis functions represent 64 different arrays of pixel values. Given a set of DCT coefficients, the inverse transform operation consists of multiplying each basis function by its corresponding coefficient, the summing of the 64 sets of pixel values. The pixel values of the basis functions, and the different distribution of the values, mean that with an appropriate set of coefficients we can generate any pattern of pixel values.

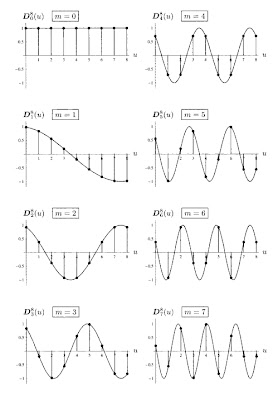
If we take this inverse approach, the forward transform is the process of finding the set of 64 coefficients that, when multiplied by the 64 coefficients, yields the original 64 pixel values.